Thường thức về Nghiên cứu khoa học dành cho nhà lâm sàng: Các đường cong sống thêm và điểm cuối

Tác giả: Vincent D. Cassidy, MD, MBA,* Ryan J. Brisson, MD, and Robert J. Amdur, MD

Department of Radiation Oncology, University of Florida College of Medicine, Gainesville, Florida

Tóm lược

Trong ung thư học, các đường cong sống thêm thường xuyên xuất hiện trên các bài báo và thuyết trình tại các hội nghị khoa học. Các nhãn thường gặp nhất của đường cong sống thêm như sống thêm toàn bộ (OS – Overall Survival), sống thêm không tái phát (RFS – Relapse Free Survival), sống thêm không bệnh tiến triển (PFS – Progression Free Survival), sống thêm không di căn xa (DMFS – Distant Metastasis Free Survival), và kiểm soát tại chỗ và/hoặc tại vùng. Cần lưu ý rằng, định nghĩa của các sự kiện cho cùng một phân tích sống thêm có thể thay đổi tùy theo tác giả. Hơn nữa, chất lượng của các đường cong sống thêm chịu tác động lớn bởi phương pháp được sử dụng để chọn điểm cuối. Bài báo này sẽ giải thích ngắn gọn các danh pháp và sự kiện điểm cuối được sử dụng cho phân tích sống thêm theo cách hữu ích với các nhà xạ trị, để có thể trình bày, phiên giải các kết quả nghiên cứu, đặc biệt các kết quả ảnh hưởng đến quyết định thực hành lâm sàng.

Kiến thức cơ bản về phương pháp thông dụng nhất trong phân tích sống thêm: Kaplan-Meier

Thuật ngữ “Phân tích sống thêm” có thể bị nhầm lẫn khi “Tử vong” không phải là một sự kiện điểm cuối (Event endpoint). Một thuật ngữ khác đặc tả hơn cho một “Phân tích sống thêm” là “Phân tích thời gian đến khi xảy ra sự kiện” (Sau đây gọi là: Phân tích thời gian đến sự kiện). Nguyên tắc cơ bản của các phân tích thời gian đến sự kiện là xem xét (1) liệu rằng sự kiện quan tâm có xảy ra hay không và (2) sự kiện quan tâm xảy ra sau can thiệp của chúng ta bao lâu. Xác suất sự kiện chưa xảy ra là một hàm sống thêm.

S là hàm sống thêm, P là xác suất, t là thời gian, và t-event là thời gian đến khi sự kiến xảy ra. Mô hình Kaplan-Meier (KM) hiện đang là phương pháp phổ biến nhất được sử dụng để ước tính hàm sống thêm và xây dựng các đường cong sống thêm. Phương pháp KM là một kỹ thuật thống kê không đòi hỏi giả định về phân phối dữ liệu, được sử dụng để ước tính hàm sống thêm của một nhóm bệnh nhân, tức là xác suất sống sót của họ tại một thời điểm nhất định sau khi điều trị. Phương pháp này tính toán bằng cách nhân liên tiếp xác suất có điều kiện sống sót đến thời điểm xảy ra biến cố tiếp theo, bắt đầu từ thời điểm ban đầu và tiến tới từng thời điểm xảy ra biến cố trong dữ liệu. Công thức tính toán như sau:

Trong đó, S là ước tính sống thêm, t(i) là thời gian xuất hiện của mỗi sự kiện thứ i, d(i) là số lượng của các sự kiện mới tại thời điểm t(i) và n(i) là số bệnh nhân còn lại, có nguy cơ xảy ra sự kiện trước khi sự kiện thứ i xảy ra (Các đối tượng gặp sự kiện thứ i sẽ được tính trong cả d(i) và n(i)). Mỗi một (1-d(i)/n(i)) là xác suất có điều kiện sống sót cho đến thời điểm xảy ra sự kiện tiếp theo.

Censoring

Để hiểu các phân tích sống thêm, chúng ta cần hiểu ý nghĩa của “Censor” một đối tượng trong phép phân tích. Censor một đối tượng nghĩa là đối tượng đó (Bệnh nhân) bị loại ra khỏi n-i nhưng không gặp sự kiện điểm cuối. Các lý do để Censor bao gồm mất theo dõi bệnh nhân giữa t(i-1) và t(i), trạng thái sự kiện điểm cuối không biết hoặc gặp phải một sự kiện điểm cuối cạnh tranh khác, ngăn chặn những đối tượng này khỏi nguy cơ xuất hiện sự kiện điểm cuối đang được quan tâm tiếp theo (Ví dụ như trong các phân tích mà “Tử vong” không phải là sự kiện điểm cuối quan tâm). Từ công thức, chúng ta thấy rằng Censoring không làm thay đổi ước tính sống thêm cho đến khi sự kiện tiếp theo xảy ra.

Các tên gọi đường cong sống thêm

Khi “Tử vong” là lựa chọn kinh điển cho sự kiện quan tâm (Chính vì vậy mà d đại diện cho số lượng sự kiện xảy ra trong công thức KM), các nhà nghiên cứu có thể áp dụng mô hình phân tích sống thêm để khảo sát các điểm cuối quan tâm khác. Các điểm cuối phức hợp cho phép nhiều hơn 1 điểm cuối tham gia cấu thành 1 sự kiện trong phép phân tích.

Việc sử dụng từ “Sống thêm” trong tên gọi của một phép phân tích với một sự kiện điểm cuối không phải “Tử vong” hoặc một sự kiện điểm cuối phức hợp bao gồm “Tử vong” có thể dẫn đến nhầm lẫn. OS có thể là phân tích sống thêm ít gây nhầm lẫn nhất khi “Tử vong” do bất kể nguyên nhân nào là sự kiện điểm cuối duy nhất. PFS là một điểm cuối phức hợp phổ biến trong nghiên cứu ung thư học, nhưng hiện chưa có một đồng thuận rộng rãi về các sự kiện điểm cuối cấu thành. Một số tác giả định nghĩa PFS là thời gian đến khi bệnh tiến triển hoặc tử vong do mọi nguyên nhân (Như vậy, gồm 2 sự kiện điểm cuối cấu thành: Bệnh tiến triển và Tử vong), trong khi những tác giả khác định nghĩa PFS là thời gian đến khi bệnh tiến triển, không tính trường hợp tử vong (1 Sự kiện điểm cuối: Bệnh tiến triển, kết quả là tử vong được xem là các đối tượng censor). Các lập luận về ngữ nghĩa đã dẫn đến các thuật ngữ tiếp theo như “Thời gian đến khi bệnh tiến triển” và “Không có bệnh tiến triển” cho các phép phân tích mà “Tử vong” không phải là một trong các sự kiện điểm cuối được quan tâm.

Lưu ý rằng việc tính toán PFS với bệnh tiến triển là sự kiện duy nhất có thể khiến phép ước tính KM thiên lệch, tốt hơn “sự thật”. Lấy ví dụ, một đường cong Thời gian đến khi bệnh tiến triển sẽ cao “giả tạo” nếu như tất cả bệnh nhân tử vong trước khi xác định bệnh tiến triển. Đó là lý do mà định nghĩa PFS với sự kiện điểm cuối phức hợp, gồm cả Tử vong và Bệnh tiến triển, được ưu tiên hơn trong nghiên cứu ung thư học. Sống thêm không biến cố (EFS – Event Free Survival) là thuật ngữ chung và ít tính thông tin nhất nếu không kèm theo định nghĩa rõ ràng. Một số tác giả sử dụng nó như là một điểm cuối phức hợp bao hàm nhiều sự kiện được quan tâm, trong khi một số khác định nghĩa EFS là một sự kiện cụ thể được quan tâm, ví dụ như biến cố tại xương có triệu chứng lâm sàng (Symptomatic skeletal EFS).

Minh họa các đường cong sống thêm và dưới típ

Bảng 1 liệt kê các thuật ngữ và sự kiện điểm cuối của nhiều típ phân tích sống thêm phổ biến trong ung thư học. Hình 1 và 2 minh họa các phân tích sống thêm cho các đoàn hệ giả định 10 bệnh nhân và diễn biến bệnh tương ứng của mỗi người bệnh, sử dụng thuật toán KM.

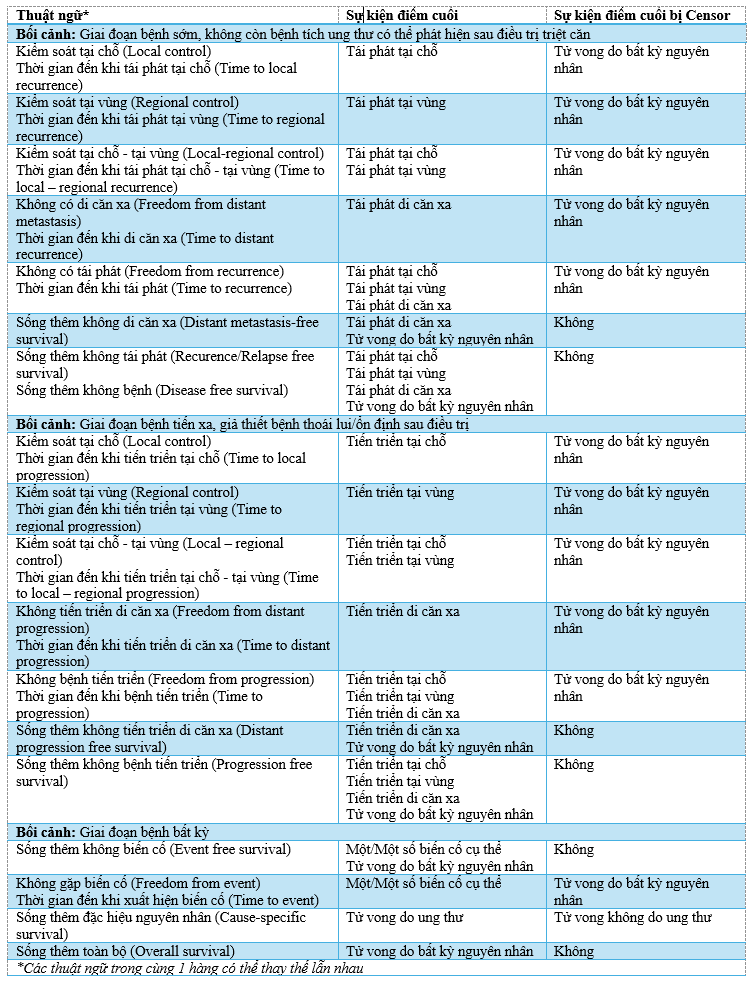
Như đã giải thích ở phần trên, các phân tích mà censor kết cục “Tử vong” có nguy cơ dẫn đến đánh giá sai lầm theo hướng tốt hơn “giả tạo” so với khi xem “Tử vong” là 1 sự kiện quan tâm. Một đường cong KM của một điểm cuối phức hợp sẽ không bao giờ “xuống dốc” “chậm hơn” so với đường cong KM của bất kỳ điểm cuối cấu thành nào. Vì vậy, nếu đường cong PFS ở phía trên đường cong OS tương ứng, thì “Tử vong” đã bị censor, và thời gian đến khi bệnh tiến triển/Không bệnh tiến triển sẽ là tên gọi phù hợp hơn cho đường cong.

So sánh các phân bố sống thêm

Trọng tâm của bài viết này là các đường cong sống thêm nói chung, và các ví dụ đã minh hoạ sống thêm trong bối cảnh của một đoàn hệ duy nhất nhằm mục tiêu đơn giản hoá. Tuy nhiên, sự khác biệt về sống thêm giữa 2 hay nhiều hơn đoàn hệ (Hoặc nhánh điều trị) thường là mối quan tâm chủ yếu trên thực tế nghiên cứu. Trong khi một số suy luận định tính có thể được dựa trên quan sát trực quan các đường cong sống thêm, có nhiều hơn các nền tảng toán học phức tạp đằng sau tiếp cận định lượng. Một thảo luận sâu rộng về các phương pháp hồi quy, như mô hình nguy cơ theo tỷ lệ (Proportional hazards models), nằm ngoài phạm vi của bài viết này, nhưng một số thuật ngữ quan trọng rất cần được làm rõ. Hàm sống thêm là một xác suất thực sự, giá trị của nó nằm trong giới hạn giữa 0 và 1. Tuy nhiên, hàm sống thêm cũng có thể được định nghĩa theo thuật ngữ hàm nguy cơ, h, là tỷ lệ thất bại và không có giới hạn trên.

Một tỷ số nguy cơ (Hazard Ratios), là một thông số thường được báo cáo về quy mô tác động trong hồi quy nguy cơ theo tỷ lệ, và là một tỷ số tỷ lệ. Các tỷ số nguy cơ (Hazard Ratios) không thể hoán đổi cho nhau với các thuật ngữ từ các mô hình thống kê khác như tỷ số odds (Odds Ratio) hay tỷ số rủi ro (Risk Ratio), mặc dù tất cả có thể có cùng một giả thuyết vô hiệu (H0) là bằng 1.

Một tỷ số rủi ro (RR) tương ứng có thể được xác định từ một tỷ số nguy cơ cho trước (HR), nhưng giá trị của nó có thể thay đổi đáng kể tuỳ theo khoảng thời gian được đánh giá.

Các khuyến nghị

Khi trình bày các đường cong hay kết quả con số của một phân tích sống thêm (Thời gian đến sự kiện), chúng tôi khuyến nghị cần kèm theo định nghĩa cho các sự kiện điểm cuối. Việc này bao gồm liệt kê đầy đủ các điểm cuối cấu thành nên một sự kiện, tiêu chuẩn cụ thể được sử dụng để xác định các điểm cuối, và bất kỳ điểm cuối cạnh tranh nào bị censor trong thuật toán phân tích. Khuyến nghị này đặc biệt quan trọng nếu sử dụng các thuật ngữ chung như EFS. Thêm vào đó, chúng tôi đề nghị tránh sử dụng từ “Sống thêm” trong tên của phép phân tích mà “Tử vong” (Đặc hiệu nguyên nhân hoặc tất cả nguyên nhân) không phải là một sự kiện điểm cuối. Tương tự như vậy, nên cẩn trọng khi đánh giá, phiên giải dữ liệu y văn, vì các đường cong sống thêm hay các tỷ số nguy cơ (HR) có thể khác biệt so với các thực hành tốt nhất.

Đọc thêm

1. Moore DF. Applied Survival Analysis Using R. Cham: Springer; 2016.

2. Jazic I, Schrag D, Sargent DJ, Haneuse S. Beyond composite endpoints analysis: Semicompeting risks as an underutilized framework for cancer research. J Natl Cancer Inst. 2016. https://doi.org/10.1093/jnci/djw154.

3. Saad ED, Katz A. Progression-free survival and time to progression as primary end points in advanced breast cancer: Often used, sometimes loosely defined. Ann Oncol. 2009;20:460-464.

4. Rich JT, Neely JG, Paniello RC, Voelker CC, Nussenbaum B, Wang EW. A practical guide to understanding Kaplan-Meier curves. Otolaryngol Head Neck Surg. 2010;143:331-336.

5. Coemans M, Verbeke G, Dohler B, Susal C, Naesens M. Bias by censoring for competing events in survival analysis. BMJ. 2022;378:e071349. https://doi.org/10.1136/bmj-2022-071349.